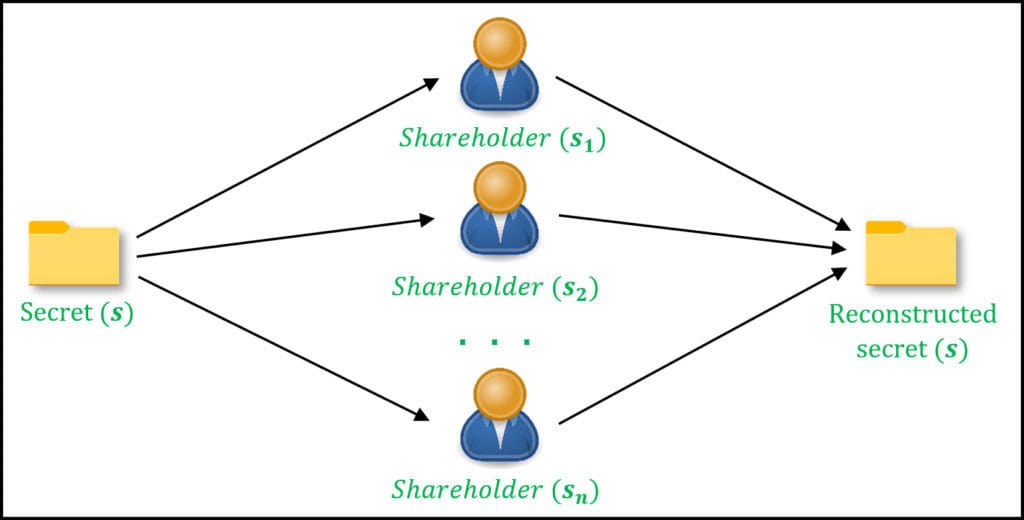
私たちのソリューションは、分散型信頼のためにShamirの秘密分散法を活用し、暗号化されたデータ上での計算のために加法的準同型暗号を利用します。最終的には、個々のデータプライバシーを損なうことなく、複数の関係者間で不正を検出できる堅牢なバックエンドシステムを構築します。
問題: プライバシー重視の世界における協調的な不正検出
不正検出はしばしば複数の情報源からのデータを比較する必要があります。しかし、プライバシーが重視される現代では、生データの共有は大きな問題です。ここに私たちの課題があります:
- 複数の銀行が顧客基盤全体で不正行為をチェックする必要がある
- どの銀行も他の銀行に顧客データを公開したくない
- 個々の記録を公開せずに共通の不正パターンを見つける必要がある
卵を割らずにオムレツを作ろうとしているように聞こえますか?それがまさにMPCが可能にすることです!
解決策: MPCとPSIが救いの手を
私たちのアプローチは、2つの主要な暗号技術を使用します:
- Shamirの秘密分散法 (SSS): 機密データを分割するため
- 加法的準同型暗号 (AHE): 暗号化されたデータ上で計算を行うため
これらを組み合わせてプライベートセットインターセクションプロトコルを作成し、データセット自体を公開せずに共通の要素を見つけることができます。
ステップ1: Shamirの秘密分散法の設定
まず、Shamirの秘密分散法を実装しましょう。このアルゴリズムは、機密データを参加者間で分配できるように分割します。
import random
from sympy import *
def generate_polynomial(secret, degree, prime):
coefficients = [secret] + [random.randint(0, prime-1) for _ in range(degree)]
return coefficients
def evaluate_polynomial(coefficients, x, prime):
return sum(coeff * pow(x, power, prime) for power, coeff in enumerate(coefficients)) % prime
def create_shares(secret, num_shares, threshold, prime):
coefficients = generate_polynomial(secret, threshold-1, prime)
return [(i, evaluate_polynomial(coefficients, i, prime)) for i in range(1, num_shares+1)]
# 使用例
prime = 2**127 - 1 # メルセンヌ素数
secret = 1234
shares = create_shares(secret, num_shares=5, threshold=3, prime=prime)
print(shares)
この実装により、秘密を複数のシェアに分割し、しきい値以上のシェアのサブセットがあれば秘密を再構築できますが、少ないシェアでは秘密について何も明らかにしません。
ステップ2: 加法的準同型暗号の実装
次に、簡単な加法的準同型暗号スキームを実装します。この例では、Paillier暗号システムを使用し、暗号化されたデータ上で加算操作を可能にします。
from phe import paillier
def generate_keypair():
return paillier.generate_paillier_keypair()
def encrypt(public_key, value):
return public_key.encrypt(value)
def decrypt(private_key, encrypted_value):
return private_key.decrypt(encrypted_value)
def add_encrypted(encrypted_a, encrypted_b):
return encrypted_a + encrypted_b
# 使用例
public_key, private_key = generate_keypair()
a, b = 10, 20
encrypted_a = encrypt(public_key, a)
encrypted_b = encrypt(public_key, b)
encrypted_sum = add_encrypted(encrypted_a, encrypted_b)
decrypted_sum = decrypt(private_key, encrypted_sum)
print(f"Decrypted sum: {decrypted_sum}") # 30になるはず
この準同型暗号スキームにより、暗号化された値を復号化せずに加算することができます。
ステップ3: プライベートセットインターセクションの実装
次に、SSSとAHEを組み合わせてプライベートセットインターセクションプロトコルを作成します:
def private_set_intersection(set_a, set_b, threshold, prime):
public_key, private_key = generate_keypair()
# set_aの各要素に対してシェアを作成
shares_a = {elem: create_shares(elem, len(set_b), threshold, prime) for elem in set_a}
# シェアを暗号化
encrypted_shares_a = {elem: [encrypt(public_key, share[1]) for share in shares] for elem, shares in shares_a.items()}
# 暗号化されたシェアを他のパーティに送信するシミュレーション
# 実際のシナリオでは、ネットワーク通信が必要です
# 他のパーティが受け取ったシェアに対して自分のセットを評価
intersection = set()
for elem_b in set_b:
possible_match = True
for elem_a, enc_shares in encrypted_shares_a.items():
reconstructed = sum(share * pow(elem_b, i+1, prime) for i, share in enumerate(enc_shares))
if decrypt(private_key, reconstructed) != 0:
possible_match = False
break
if possible_match:
intersection.add(elem_b)
return intersection
# 使用例
set_a = {1, 2, 3, 4, 5}
set_b = {3, 4, 5, 6, 7}
threshold = 3
prime = 2**127 - 1
intersection = private_set_intersection(set_a, set_b, threshold, prime)
print(f"Intersection: {intersection}")
この実装により、2つのパーティが自分のセットを公開せずにセットの交差を見つけることができます。
すべてをまとめる: 不正検出システム
これで、MPCベースのプライベートセットインターセクションを使用して簡単な不正検出システムを作成しましょう:
class Bank:
def __init__(self, name, suspicious_accounts):
self.name = name
self.suspicious_accounts = set(suspicious_accounts)
class FraudDetectionSystem:
def __init__(self, banks, threshold, prime):
self.banks = banks
self.threshold = threshold
self.prime = prime
def detect_common_suspicious_accounts(self):
if len(self.banks) < 2:
return set()
common_suspicious = self.banks[0].suspicious_accounts
for i in range(1, len(self.banks)):
common_suspicious = private_set_intersection(
common_suspicious,
self.banks[i].suspicious_accounts,
self.threshold,
self.prime
)
return common_suspicious
# 使用例
bank_a = Bank("Bank A", [1001, 1002, 1003, 1004, 1005])
bank_b = Bank("Bank B", [1003, 1004, 1005, 1006, 1007])
bank_c = Bank("Bank C", [1005, 1006, 1007, 1008, 1009])
fraud_system = FraudDetectionSystem([bank_a, bank_b, bank_c], threshold=3, prime=2**127 - 1)
common_suspicious = fraud_system.detect_common_suspicious_accounts()
print(f"Common suspicious accounts: {common_suspicious}")
このシステムにより、複数の銀行が個々の疑わしいアカウントリストを公開せずに、協力して潜在的な不正アカウントを検出できます。
考えるべきこと: 影響と考慮事項
これを本番環境で実装する前に、考慮すべき点があります:
- パフォーマンス: MPCプロトコルは計算負荷が高い場合があります。大規模なデータセットに対してどのように最適化しますか?
- ネットワーク通信: 私たちの例ではローカル計算を想定しています。実際には、関係者間の安全なネットワーク通信を処理する必要があります。
- セキュリティモデル: 私たちの実装は半誠実な関係者を想定しています。悪意のある攻撃者に対してどのような変更が必要ですか?
- 規制遵守: このアプローチはGDPRやCCPAなどのデータ保護規制とどのように整合しますか?
まとめ: プライバシー保護計算の力
セキュアマルチパーティ計算とプライベートセットインターセクションで可能なことの表面をかじっただけです。これらの技術を活用することで、個人のプライバシーを尊重する強力な協力システムを作成できます。
データプライバシーの世界では、単にコードを書くのではなく、信頼を構築しています。次に誰かがプライバシーとデータの有用性は相反すると言ったら、自信を持って「ホモモルフィックに暗号化されたビールを持ってきて!」と言えます。
コーディングを楽しんで、あなたの計算が永遠に安全でありますように!
"In God we trust. All others must bring data." - そして今、MPCのおかげで、実際にデータを持ってこなくてもデータを持ってくることができます!