エヴァリスト・ガロアの名において、何を話しているのか?
暗号の世界に飛び込む前に、ガロア体が何であるかを分解してみましょう。若きフランスの数学者エヴァリスト・ガロアにちなんで名付けられたこれらの体は、特別な代数的性質を持つ有限の要素集合です。ちなみに、彼は20歳で決闘で亡くなったそうです。
簡単に言えば、特定のルールに従って数が遊ぶ遊び場を想像してください。これらのルールは、数を加えたり、引いたり、掛けたり、割ったりしても(ゼロで割ることはできませんが)、常に同じ遊び場の中で別の数になることを保証します。
暗号との関係:なぜガロア体が重要なのか
「面白い話だけど、これがどうして私の猫のミームを守ることに関係するの?」と思うかもしれません。良い質問です!ガロア体は、あまり知られていないがますます重要になっているいくつかの暗号システムの基盤です。なぜこれが注目されているのか、以下に示します:
- 効率性: ガロア体での操作は非常に速く効率的で、リアルタイムの暗号化にとって重要です。
- 耐性: 特定の種類の暗号攻撃に対して強い耐性を提供します。
- 柔軟性: 異なるサイズのガロア体を使用して、さまざまなレベルのセキュリティを作成でき、異なるニーズに適応できます。
実際の暗号システムでのガロア体の活用
ガロア体を活用している暗号システムをいくつか見てみましょう:
1. 高度暗号化標準 (AES)
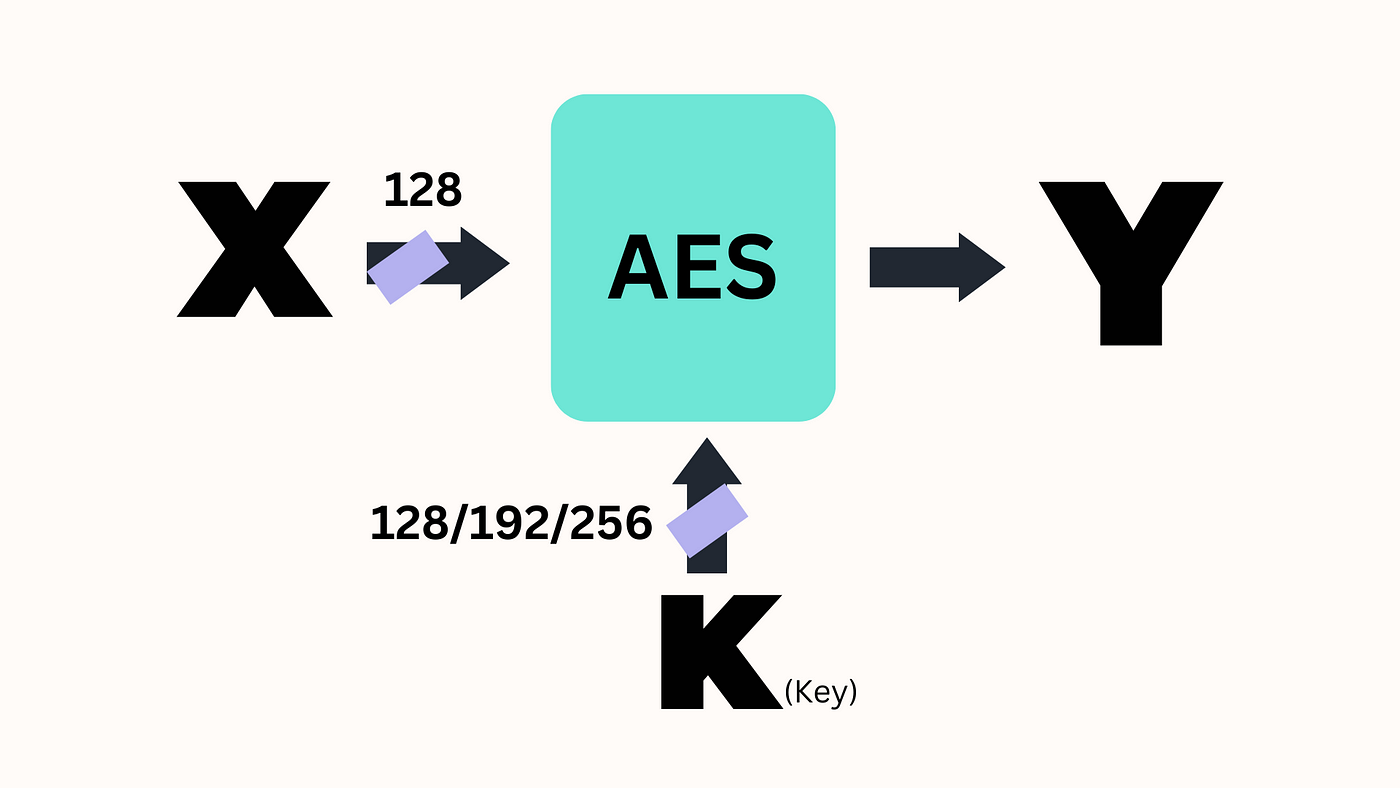
そう、あのAESです。次世代というわけではありませんが、AESはMixColumnsステップでガロア体GF(2^8)の操作を使用しています。これにより、安全な暗号化に必要な混乱と拡散が生まれます。
2. リード・ソロモン誤り訂正
主にデータ伝送と保存の誤り訂正に使用されますが、リード・ソロモンコードはガロア体の算術に基づいており、特に秘密分散スキームで暗号にも応用されています。
3. 楕円曲線暗号 (ECC)
ECCは有限体、しばしばガロア体上で動作します。これにより、RSAと同等のセキュリティレベルを維持しながら、より小さな鍵サイズを可能にします。
次のフロンティア:ポスト量子暗号
ここからが本当に面白いところです。量子コンピュータが現れ、現在の多くの暗号化方法を破る可能性がある中で、暗号学者たちは量子耐性アルゴリズムを開発するためにガロア体に目を向けています。
コードベースの暗号
有望な分野の一つがコードベースの暗号で、ガロア体の操作に大きく依存しています。例えば、McEliece暗号システムは、有限体上の誤り訂正コードを使用して、量子耐性があると考えられる公開鍵暗号システムを作成します。
以下は、コードベースの暗号でガロア体がどのように使用されるかの簡単な例です:
import galois
# サイズ2^8のガロア体を作成
GF = galois.GF(2**8)
# ランダムなメッセージを生成
message = GF.Random(10)
# ランダムな誤りベクトルを生成
error = GF.Random(10)
# エンコードと誤りの追加をシミュレート
encoded_message = message + error
# 実際には、デコードにはガロア体の特性を使用した複雑なアルゴリズムが必要
decoded_message = encoded_message - error
print(f"元のメッセージ: {message}")
print(f"デコードされたメッセージ: {decoded_message}")
print(f"等しいか? {all(message == decoded_message)}")
これはもちろん非常に簡略化された例です。実際のコードベースの暗号システムは、はるかに複雑な操作と大きなフィールドサイズを含みます。
課題と考慮事項
ガロア体で暗号コードをすべて書き直す前に、いくつかの課題を考慮しましょう:
- 複雑さ: ガロア体を扱うには抽象代数学のしっかりとした理解が必要です。簡単ではありません。
- 実装: ガロア体の算術の効率的な実装は、これらの操作に最適化されていないハードウェアでは難しいことがあります。
- 標準化: 多くのガロア体ベースの暗号システムはまだ研究段階にあり、広く標準化されていません。
では、何がそんなに重要なのか?
ガロア体は単なる数学的な好奇心ではありません。これらは、より速く、より効率的で、潜在的に量子耐性のある新世代の暗号システムの基盤を提供しています。データセキュリティがこれまで以上に重要な時代に突入する中で、これらの数学的構造は私たちのデジタル生活を安全に保つ上でますます重要な役割を果たすでしょう。
暗号愛好家、セキュリティ専門家、またはパーティーで賢く見せたいだけの人であっても、現代の暗号におけるガロア体の役割を理解することは、間違いなく価値があります。次のデータセキュリティの突破口は、これらの有限体から生まれるかもしれません。
"数学を行う芸術は、すべての一般性の芽を含む特別なケースを見つけることにある。" - デイビッド・ヒルベルト
そして、現代の暗号の場合、その特別なケースはガロア体かもしれません。次に誰かが暗号の未来について尋ねたとき、「それはすべてガロアについてだ」と自信を持って言うことができます。
さらなる学習
ガロア体とその暗号への応用に興味を持ち、さらに深く掘り下げたい場合は、以下のリソースを参考にしてください:
暗号の世界では、今日の最先端が明日の陳腐化です。好奇心を持ち続け、学び続けてください。もしかしたら、次の大きな暗号の発見をするのはあなたかもしれません。ガロアがあなたと共にありますように!